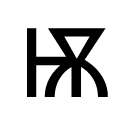
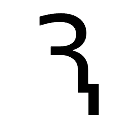On the Subject of Arithmelogic

(Math is fun) ⊻ (Bomb is armed) = True.

• This module contains a submit button with a symbol on it, three pressable displays with four numbers each, and a display showing a three-element logical statement.
• Each of the symbols within the three-element logic statement corresponds to a certain value, as shown on Table A.
• The submit button has a symbol that corresponds to a condition, also on Table A. Numbers that meet that condition are considered TRUE, others are considered FALSE.
• You can cycle through each display’s numbers by pressing that display. At least one of the numbers in each display, when added to the associated symbol’s value, will make that element true, and at least one will make it false. To submit an answer, press the submit button.
• IMPORTANT: When submitting, the symbol’s value for an element will be added to the number in the screen above it before the three-element statement is evaluated. The parenthetical statement will be evaluated first.
• If, when submitting, the statement as a whole evaluates to true AND, for each final calculated element within the three-element statement, there is no higher number for that button’s display which would keep the true/false value of that element the same, the module will be disarmed. Otherwise, a strike will be given.

Table A: Symbols and their meanings

Symbol	Value if in statement	Condition if submit button
	The submit symbol’s position in the manual’s table	The number is even
	The earliest position of serial number letters in the English alphabet	The number is a multiple of 7 or 13
	The average serial number digit, rounded up	The number modulo 3 = 1
	The number of indicators	The number is prime
	The number of battery holders	Any of the number’s digits are odd
	Triple the number of lit indicators	The number modulo 5 = 2 or 4
	The day of the month when the bomb was activated	The number’s digits add up to a number from 9 to 13, inclusive
	The lowest serial number digit plus five	The number’s last two digits are within two of each other
	The total number of ports	The number modulo 7 = 1, 3, or 6
	The number of unlit indicators times four	The number contains a 3 or 6
	The number of serial number consonants times five	The number’s digital root is odd

Table A cont’d

Symbol	Value if in statement	Condition if submit button
	The number of batteries	The number is a multiple of 4
	The sum of the serial number’s digits	The number’s digits add up to an odd number
	The latest position of serial number letters in the English alphabet	The number is odd
	The total number of modules on bomb modulo 25	The number’s digits don’t add up to a number from 7 to 11, inclusive
	The number of serial number vowels times six	The number is a multiple of 6
	The number of batteries plus indicators	The number’s digital root is even
	The number of lit indicators plus port plates	The number is composite
	The number of port plates	The number’s digits add up to an even number
	The highest serial number digit	The number contains a 2 or 9
	Fifteen	The number modulo 4 = 1
	The number of unlit indicators plus battery holders	The number’s last two digits are at least five apart

Appendix of Things to Know

Logical Connective Symbol List

Logical Connective	Symbol	Logic Gate Equivalent	Meaning
Conjunction	∧	AND	Returns true if all inputs are true. Else returns false.
Disjunction	∨	OR	Returns true if any input is true. Else returns false.
Exclusive Disjunction	⊻	XOR	Returns true if exactly one input is true. Else returns false.
Alternative Denial	|	NAND	Returns false if all inputs are true. Else returns true.
Joint Denial	↓	NOR	Returns false if any input is true. Else returns true.
Biconditional	↔	XNOR	Returns false if exactly one input is true. Else returns true.
Implication (Left)	→	-	Returns false when left input is true and right input is false. Else returns true.
Implication (Right)	←	-	Returns false when left input is false and right input is true. Else returns true.

• Modulo is the remainder from a division problem; 10 modulo 3 is 1.
• The digital root is the continual summing of a number’s digits until the result is a single digit number from 0 to 9.
• Vowels are A, E, I, O, and U.
• Prime numbers from 2 to 200 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, and 199. If your number is greater than 200, the first thousand prime numbers can be found here. Composite integers are integers greater than 3 and not prime.