On the Subject of Dimension King
And you thought the nightmare would end with Ultracube and UltraStores...
The module shows a 4D or 5D shape, with the base shape having three to five vertices.
Getting the info required to solve this module:
First of all, determine the dimension count.
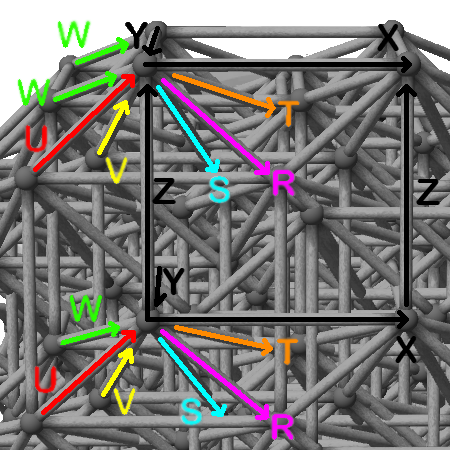
Then, read the sequence of five rotations of the shape. There is a sixth rotation, which is a quintuple rotation, before the sequence restarts.
From the following list of rotation-axis letters, determine the value of each rotation-axis letter:
X=0, Y=1, Z=2, W=3, V=4, ...
Now calculate the rotation values Rn, where n is the rotation position starting at 1, ‘a’ being the value of the first rotation-axis letter, and ‘b’ being the second:
Rn = a * {dimensionCount} + b
Now determine the first two Schläfli numbers, S1 and S2:
The first Schläfli number specifies how many vertices are required to make up a base face.
The second Schläfli number determines how many faces enclose every vertex.
Coordinate system:
Dimension King uses the N-d coordinate system version 1.0 which was designed to work with up to 9 dimensions. Check the last page for further explanation.
Note: The KTANE bomb factory recently hired new staff and the person that plugs in this module can’t decide where the status light should be, so this module may be rotated. Because the coordinate system is relative to the module, the axes will rotate if the module is rotated.