モジュール詳細：カルノー図

「待って、あれって熱力学の設定に出てくるあの人？」

• このモジュールには5×5マスのスクリーンと、1, 2, 3, 4, D, Sと書かれた6つのボタンがある。
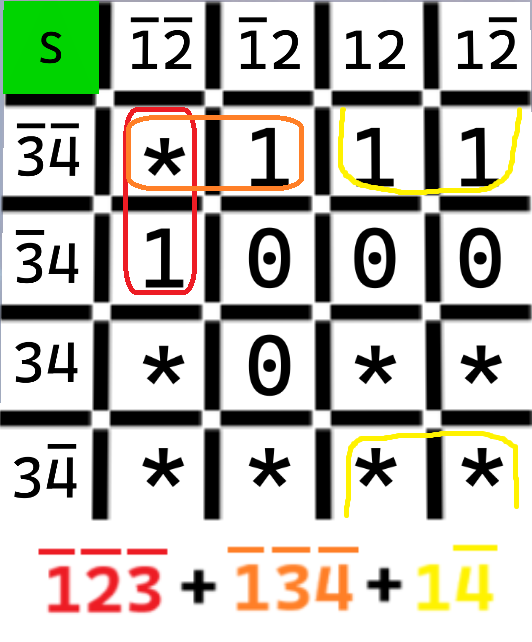
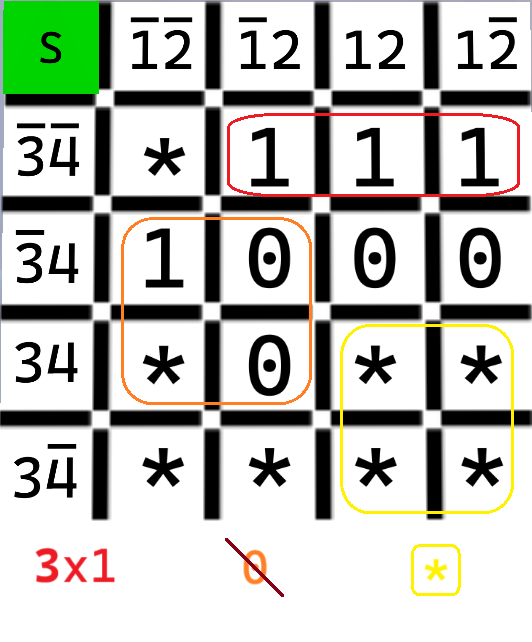
• このモジュールを解除するには、スクリーンに表示されたカルノー図(0, 1, *で作られた4×4の行列)を表す論理式を送信する必要がある。論理式は変数で構成される。肯定変数は1, 2, 3, 4であり、否定変数は1, 2, 3, 4である。
• 対応するボタンを1回押すと肯定変数が入力される。対応するボタンを2回押すと否定変数が入力される。
• Sボタンを1回押すと+が入力される。Sボタンを2回押すと論理式が送信される。
• Dボタンを押すと最後に入力された内容が削除される。

論理式の求め方

• 以下、両辺の長さが2のべき乗(1, 2, 4)である行列上の長方形をグループと呼ぶ。
• 1を1つ以上含み、0を1つも含まないグループを見つける。
• 見つけたグループに関する論理式の項を計算するには、グループのすべてのマスの共通変数を入力する。共通変数の求め方は以下の通りである。
  • 1つのマスに関する変数を取る(例えば次のページにある図のC2は1234)。
  • グループ内の他のマスでも同じことを行い、変数を比較する。肯定変数と否定変数のどちらも存在する変数を考慮から除外する。
  • グループ内のすべてのマスで同じことを行い、考慮に残った変数で比較を続ける。 新たなマスと比較する際、既に考慮から外した変数は考慮しなくてよい。
• いくつかのグループで行列上のすべての1を覆えれば、各グループの式を+記号で連結することで最終的な論理式を得られる(例えば13+234)。

備考

• このモジュールでは、行列上に最大4個ずつ0, 1が表示される。

• 行列は上辺と下辺が、左辺と右辺が繋がっている。
• このモジュールは、送信された式が最適化されているかどうかは判定しない(つまり、有効な式であればどういったものでも送信できる)。
• グループは*だけを含むことはできない。
• *か1を含むマスは複数のグループに含むことができる。
• 行列中に1がない場合、falseを送信しなければならない。そのときは、画面が空の時にSを押す。
• 行列中に0がない場合、trueを送信することが解答の1つである(そのときは、行列全体を覆う式を提出する必要がある。例えば、1+1(1だけでなく、どんな変数でもよい)のようにすればよい)。

例

	：1234と1234の共通変数は123である。
	橙：グループは重ねられる。
	：グループは行列を回り込める。
	：片方の辺の長さが2のべき乗ではないので、無効なグループである。
	橙：グループは0を含むことはできない。
	：グループは*だけを含むことはできない。