On the Subject of A Password Module That Shouldn't Be Touched

This thing is not as secure as 256-bit security, I think.

In order to solve the module, a password is required to be entered in the input phase.

Preface

• F1 will serve as a submit/stage-advance button.
• F2 clears your input.

Activating The Module

If Bamboozled Again, Ultimate Cycle, or UltraStores is present, the input is simply *dead*. This can be inputted using "88DDEEAADD88".

Otherwise, take the serial number, convert the digits using A0Z25 (table for convenience), and convert everything to lowercase. You can input this by pressing each letter twice on the module.
For example, "UX4TA2" would be inputted as "UUXXEETTAACC".

Digit	0	1	2	3	4	5	6	7	8	9
Letter	a	b	c	d	e	f	g	h	i	j

Stage Phase

The module's representation of the increase factor (I) can be anywhere from base 5 to base 16. You can use the base converter below to convert from some specified base back to decimal. Case does NOT matter in the boxes.
(If the result is -1, the input is invalid.)

Display: Base: Result:

The calculated value for a stage is calculated with the formula:

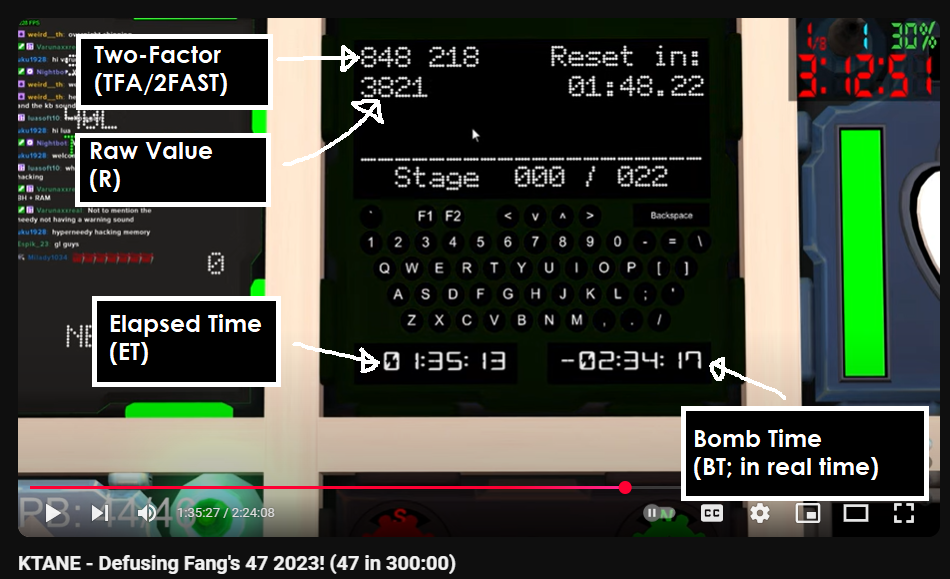
C = I + (TFA % 9) + (BT % 60 + ET % 60)

• C is the calculated value.
• I is the average increase factor, in base-10.
• TFA is the 2FAST, in the top-left.
• BT is amount of bomb time remaining in real time upon advancing from this stage, in the bottom-right.
• ET is elapsed time since the module initialized upon advancing from this stage, in the bottom-left.

A stage regenerates its information every 2 minutes, so work quickly.

Input/Submission Phase

The number of stages, S, is based on the number of modules, M:

S = max(floor(M / 2), 5)

The number of stages should match S. Once you've calculated your C-values for each stage, enter the input phase, where each stage has a final value, F:

F = (C + 60 * (60 * h + m) + s) % 94 + 33

• h is the number of elapsed hours.
• m is the number of elapsed minutes.
• s is the number of elapsed seconds.
• This can be seen in the bottom-left, and will stay constant.

If the previous stage's F-value matches this one, add 1 to F; treat 127 as 125.

Convert all F-values to characters:

F=	033	034	035	036	037	038	039	040	041	042	043	044	045	046	047
Symbol	!	"	#	$	%	&	'	(	)	*	+	,	-	.	/
Input	11	''	33	44	55	77	'	99	00	88	==	,	-	.	/
F=	048	049	050	051	052	053	054	055	056	057	058	059	060	061	062
Symbol	0	1	2	3	4	5	6	7	8	9	:	;	<	=	>
Input	0	1	2	3	4	5	6	7	8	9	;;	;	,	=	.
F=	063	064	065	066	067	068	069	070	071	072	073	074	075	076	077
Symbol	?	@	A	B	C	D	E	F	G	H	I	J	K	L	M
Input	//	22	A	B	C	D	E	F	G	H	I	J	K	L	M
F=	078	079	080	081	082	083	084	085	086	087	088	089	090	091	092
Symbol	N	O	P	Q	R	S	T	U	V	W	X	Y	Z	[	\
Input	N	O	P	Q	R	S	T	U	V	W	X	Y	Z	[	\
F=	093	094	095	096	097	098	099	100	101	102	103	104	105	106	107
Symbol	]	^	_	`	a	b	c	d	e	f	g	h	i	j	k
Input	]	66	--	`	AA	BB	CC	DD	EE	FF	GG	HH	II	JJ	KK
F=	108	109	110	111	112	113	114	115	116	117	118	119	120	121	122
Symbol	l	m	n	o	p	q	r	s	t	u	v	w	x	y	z
Input	LL	MM	NN	OO	PP	QQ	RR	SS	TT	UU	VV	WW	XX	YY	ZZ
F=	123	124	125	126	If you're Eltrick (otherwise want to be like him), all characters are from this string: !"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~
Symbol	{	|	}	~
Input	[[	\\	]]	``

Solving Strategy, With Example

As of writing this manual, the only challenge bomb solve that has Password Mutilator EX is Fang's 47 2023, with Danielstigman as the defuser and Varunaxx as the expert who did the module.

Activating the module is easy, as you can refer to the first page of this manual. The hard part starts when you press F1, however. There is a lot to unpack, but you can follow this procedure:

1. Read the raw value once ("R1").
2. Wait 5 seconds, then read the raw value again ("R2"). If R2 loops around and is less than R1, prepend a 1 to R2.
3. Wait until the display loops back to less than 4 digits. Take the largest digit that appears (0-9, A-F).
4. This is your base. Convert R1 and R2 from that base to decimal.
5. Subtract R1 from R2, and then divide the result by 5. Round the result to get the increase factor. You can think of this using this formula (rounding accordingly):

I = (R2 - R1) / 5

6. Write down the Two-Factor ("TFA"). It may look like 2 3-digit numbers, but concatenate them into a single 6-digit number.
7. Press F1. You now have 5 seconds to write down the last 2 digits of the BT and ET before they disappear.
8. Plug the obtained values into the equation for your C-value! You are now done with this stage.

Now that you have a C-value for this stage, repeat for subsequent stages, until you get to the pre-input phase. C-values do not change between stages.

In the example from the first stage of Password Mutilator EX from Fang's 47 2023, Danielstigman read the raw value at BT=-02:34:24 (9573) and BT=-02:34:19 (2607). Since the raw value looped around midway through, it technically exceeded 10000. In addition, there was no base conversion because there was a 9 but no A (base-10). Therefore, R2 is actually 12607. The increase factor is equal to:

I = (12607 - 9573) / 5 = 606.8 ≈ 607

Danielstigman read the TFA (848218), and then pressed F1 to advance a stage, reading ET = 36 and BT = 54. Using this information, the calculated value is:

C = 607 + (848218 % 9) + (54 % 60 + 36 % 60) = 701

Once you obtain every C-value you need, it is now time to calculate F-values. It's worth mentioning that the elapsed time will not change in this phase.

Once you obtain all F-values, they need to be converted into characters before inputting.

Back to the aforementioned example, when Danielstigman entered input phase, the elapsed time was 1:49:29. The final value for the first stage is:

F = (701 + 60 * (60 * 1 + 49) + 29) % 94 + 33 = 65

65 translates to the character "A", which was inputted into the module in the input phase.

The final answer for the module was "Ak&2D&]V/R@C\?.)GCRu{5>" (ignoring quotes), which is inputted as "AKK772D77]V/R22C\//.00GCRUU[[5.." (ignoring quotes).

Danielstigman and Varunaxx went on to solve the module with no strikes.