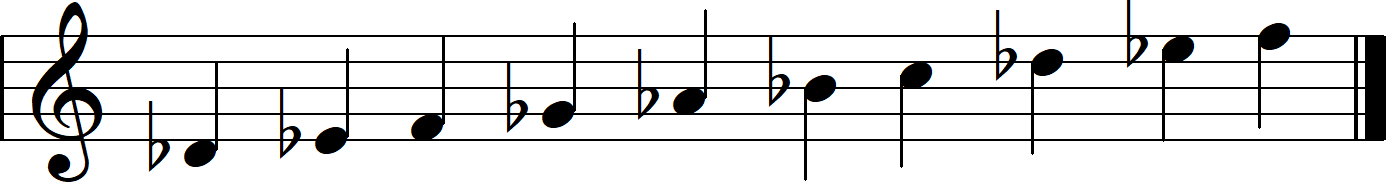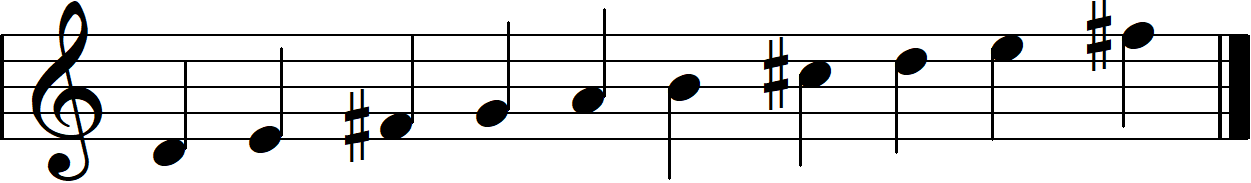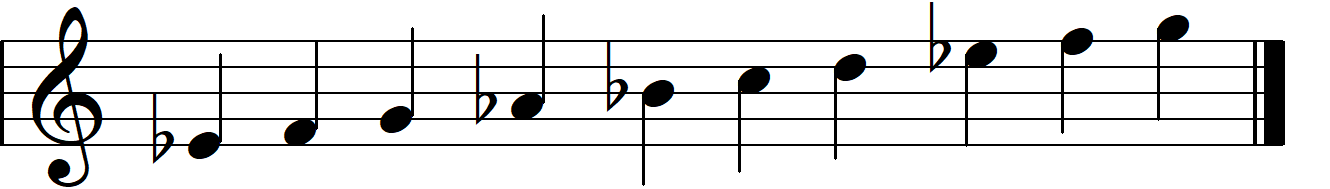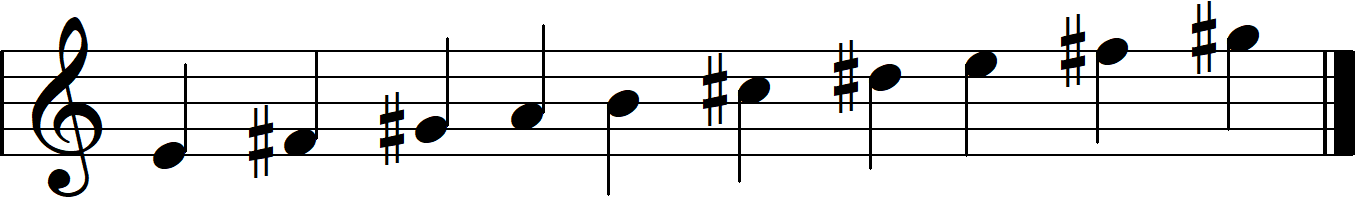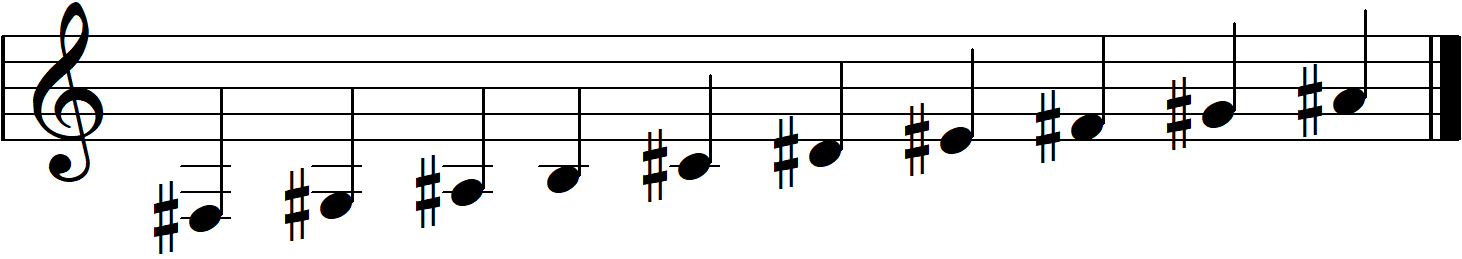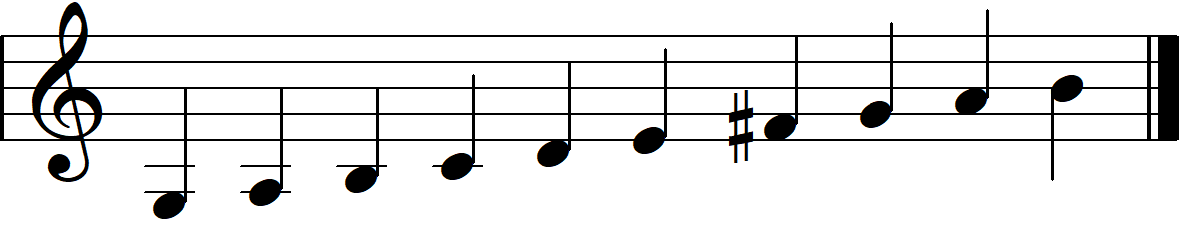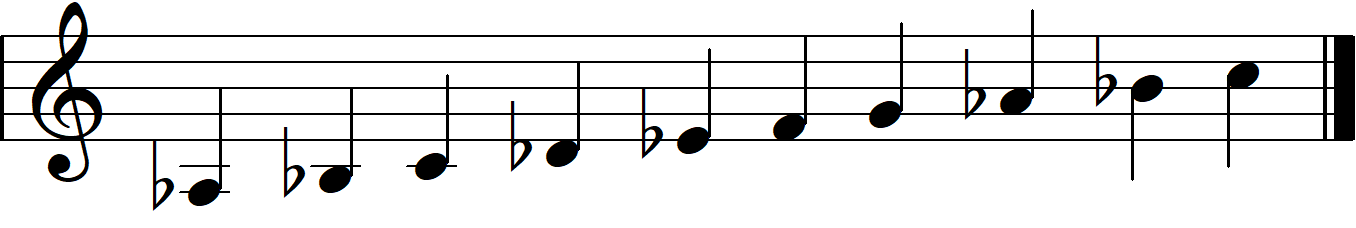On the Subject of Scalar Dials

*Twist* Wait, did I hear something? *Twist*

On the module, you will see 3 dials, each with a small screen above it, a larger screen displaying 3 notes and a clef, and a submit button on the top left.

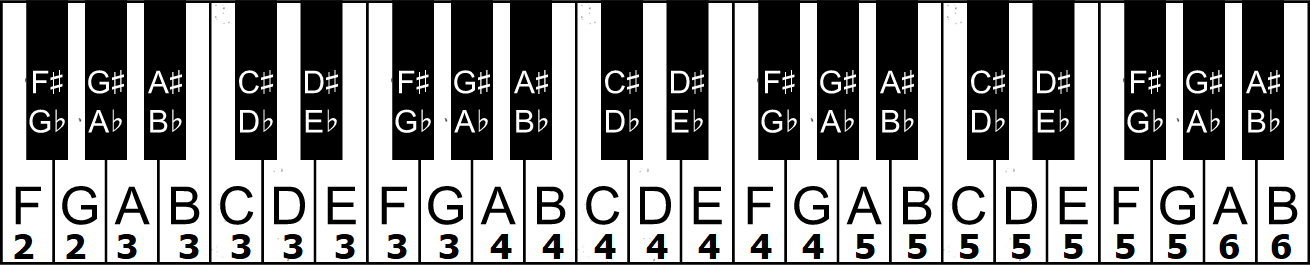
Each dial cycles from 0 - 9 with a note displayed on the screen above it. When you turn the dial, it will play a tone that is part of a scale.

Pressing the screens above the dials will play the tone the dial is currently on. Pressing the larger screen will play one of the 3 notes depending on the time remaining.

The dials are read from left to right.

Set each dial to the correct position and submit it at the correct time to disarm the module.

Submitting the wrong combination and/or submitting it at the wrong time will cause it to strike.

Step 1: Initial Positions

For each dial, do the following:

• A: The nth note the larger screen is playing is found by doing this equation: 3 - (Minutes Remaining % 3).
• B: Figure out which major scale the nth dial is playing. This can be done by setting the dial to the lowest tone it plays and comparing it with the note the larger screen is playing.
• C: Use the scale of the nth dial as the row and the nth note on the larger screen as the column for the table below.
• D: The number you get from the intersection in the table is the initial position of that dial.

	C/B#	C#/Db	D	D#/Eb	E/Fb	F/E#	F#/Gb	G	G#/Ab	A	A#/Bb	B/Cb
C	8	1	3	1	6	9	5	7	4	0	2	0
Db	1	2	4	3	6	2	9	5	1	7	0	8
D	3	7	4	2	3	1	8	5	2	6	9	0
Eb	1	9	5	4	3	0	7	2	8	4	3	6
E	6	4	8	5	4	2	3	1	0	5	7	9
F	2	4	5	1	6	5	0	6	8	9	7	3
F#	6	5	2	0	7	1	3	8	6	4	7	9
G	2	4	8	9	5	3	7	1	8	7	0	6
Ab	3	0	5	2	1	9	8	8	6	9	4	7
A	7	5	3	0	9	6	8	9	4	2	0	1
Bb	4	1	0	8	6	2	1	7	5	0	3	9
B	0	1	1	6	2	2	8	9	7	5	3	4

C Scale

Db Scale

D Scale

Eb Scale

E Scale

F Scale

F# Scale

G Scale

Ab Scale

A Scale

Bb Scale

B Scale

Step 2: Final Positions

For each dial do the following:

• A: Find the exact note on the nth screen on the sheet music below.
• B: Find the exact note on the nth note on the large screen on the sheet music below.
• C: Count the number of notes inbetween these 2 notes you found on the sheet music. But only count the notes that are:
• If the nth screen's background is white, count the notes that are on the lines (Red Notes).
• Otherwise, count the notes that are in the spaces (Blue Notes).

• D: Modulo the number by 10 and set the nth dial to that number.

Step 3: Submit Time

Find out the interval between the note that the dial is currently playing at and the screen's note. The screen's clef is the same thing as the larger screen's clef.

Note: If the 2 notes have a difference more than or equal to an octave, take the higher note and move it down an octave until it is within P1 - M7 range.

Do this for all the dials/screens and use the interval and which nth dial/screen to get a number on the table below:

	1st	2nd	3rd
P1	9	6	7
m2	13	11	12
M2	5	5	13
m3	8	3	4
M3	12	9	8
P4	2	12	11
TT	10	7	6
P5	3	10	2
m6	11	8	10
M6	6	13	9
m7	4	2	3
M7	7	4	5

Multiply the 3 numbers together and turn it into binary. This can be done by dividing the number by 2 and writing the remainder (which is 1 or 0) to the left of any previous digits. Keep doing this until the number is 0:

Example

780 / 2 = 390 REM: 0
390 / 2 = 195 REM: 0
195 / 2 = 97 REM: 1
97 / 2 = 48 REM: 1
48 / 2 = 24 REM: 0
24 / 2 = 12 REM: 0
12 / 2 = 6 REM: 0
6 / 2 = 3 REM: 0
3 / 2 = 1 REM: 1
1 / 2 = 0 REM: 1
Binary: 1100001100

If the number of digits in the binary is not a multiple of 3, add zeros to the front of the binary until the number of digits is a multiple of 3.

Then take the background colors of the 3 screens in reading order and write them over each digit of the binary, writing the 3 color sequence over and over until each digit has a color associated with it.

Example

Binary: 001100001100
Color Pattern: White Black Black (WBB)

W	B	B	W	B	B	W	B	B	W	B	B
0	0	1	1	0	0	0	0	1	1	0	0

Let S = 0, for each digit/color combination:

• If the color is white and the digit is 1, add 1 to S.
• Otherwise if the color is black and the digit is 0, add 1 to S.

Take S, modulo it by 10, and submit when the last seconds digit on the countdown timer is equal to this number.

Clefs, Notes, Accidentals, Oh My!

A clef is a musical symbol used to indicate the pitch of written notes. They are written at the beginning of every line in sheet music. Down below are the notes that are played for each clef. The exact letter/number pair references to a key on the keyboard down below.

Treble Clef Notes

Bass Clef Notes

Alto Clef Notes

Keyboard

When you see a # or b symbol is to the left of a note, that note is raised or lowered by 1 half-step.

A half-step is the key that is adjacent to that key on the keyboard. For example, an G# is the black key between a G key and a A key. An Bb is the key that is between a A key and a B key. This means an E# is the same thing as a F key and vice versa when it is Fb. Same thing for B# and Cb.

Intervals

An interval is the distance between 2 pitches. There are 12 distinct intervals that our ears can differentiate. The following notes corresponds to the audio files below in reading order:

Interval	P1	m2	M2	m3	M3	P4	TT	P5	m6	M6	m7	M7
Difference of half-steps	0	1	2	3	4	5	6	7	8	9	10	11

However, at times the 2 tones can sound like they have a difference higher than M7. In that case, either take the lower tone up an octave or take the higher tone down an octave until it is within the P1 - M7 range.

An octave consists of a difference of 12 half-steps. The 2 notes will be similiar in pitch to one another like a P1 but one note is higher than the other.

Do the same with the notes written on the module when taken the difference between the 2 notes.